Dit is hoe een simpel en elegant algoritme Google Maps mogelijk maakt

​Algoritmes zijn een wetenschap van bekwaamheid. Het zijn natuurlijke manifestaties van logische beredenering. Denk bijvoorbeeld aan volledige inductie. Een goed algoritme is als een vluchtige en vernietigende momentopname midden in de ziel van een probleem. Een jungle van eigenschappen en relaties wordt een eenvoudige herhaling, die grenzeloze chaos en complexiteit in recursieve stappen produceert. Het vergt dan ook vaardigheid om door die diepe complexiteit heen te kunnen kijken.

Pioneerprogrammeur Edsger W. Dijkstra, had deze vaardigheid. Zijn EWD's (zijn handgeschreven manuscripten, vernoemd naar zijn initialen) zijn nog steeds één van de slimste algoritmes uit de informaticawetenschap. Hij was een voorstander van eenvoud en elegantie in de wiskunde. Hij geloofde er min of meer in dat ieder ingewikkeld probleem een toegankelijke 'begane grond' zou moeten hebben. In de wiskunde zag hij een perfect hulpmiddel om deze problemen te vinden en te exploiteren.

Van 1952 tot aan 1962 heeft Dijkstra als wetenschappelijk programmeur bij het mathematisch centrum in Amsterdam gewerkt. Daar heeft hij gewerkt aan de programmering van ARRA en later aan die van de ARMAC. Dit zijn de eerste computers ooit gebouwd in Nederland. in 1956 begon hij aan het proefschrift voor de ARMAC, wat hij twee jaar later publiceerde. Na die publicatie stond Dijkstra voor een nieuwe uitdaging.

"Een demonstratie voor mensen die geen wiskundige vaardigheden hebben is lastig. Je moet een demonstratiemethode hebben om het voor hun ook begrijpelijk uit te leggen," zei Dijkstra vlak voor zijn overlijden in een interview in 2002. "Ze moeten de uitkomst van een probleem kunnen begrijpen. Daarom heb ik een programma ontworpen wat de kortste route tussen twee steden in Nederland laat zien. Daarvoor heb ik een kaart met 64 steden gebruikt."

"Wat is de snelste weg van Rotterdam naar Groningen?," zei Dijkstra. "Dat is een algoritme voor de snelste weg, wat ik in zo'n 20 minuten heb ontworpen."

Dit is precies wat Google Maps nu voor ons doet, alleen we denken totaal niet na over de complexe taak die dit mogelijk maakt. Dat is de functie van de kortste weg vinden, een belangrijk kenmerk van de grafentheorie. Die theorie wordt bijvoorbeeld gebruikt om een schematische routekaart te maken tussen een aantal plaatsen met de afstanden daartussen. Er zijn ontzettend veel hedendaagse applicaties gebaseerd op deze theorie. De theorie resulteert (informeel gezien) als een explosie van combinaties, waarin het aantal verschillende combinaties wordt onderzocht in exponentiele groei.

Het resultaat van zo'n explosie is dat problemen - zoals het probleem van de kortste weg - zo snel groeien dat de mogelijkheden vrijwel ontelbaar worden en er daardoor ontelbare tijd nodig is om ze op te lossen. Er zijn slechts een handvol knooppunten in een bepaalde map of grafiek nodig om te kunnen resulteren in miljarden combinaties.

Het algoritme van Dijkstra is waarschijnlijk het makkelijkst uit te leggen met een voorbeeld. Zie het grafiek hieronder, waarin de cijfers het gewicht van iedere verbinding voorstellen. (Het gewicht zou eenvoudig gezegd de afstand kunnen voorstellen /of in principe iedere relatieve vereiste die nodig is voor het reizen tussen de bepaalde verbindingen, die we - doelmatig - zouden willen minimaliseren.) Om te beginnen noemen we punt s, onze startpositie. Er is 0 km (of welke inspanning dan ook) nodig om hier te komen, want: startpositie. Vervolgens kijken we naar de aangrenzende knooppunten van s. Deze moeten in feite 'verkend' gaan worden.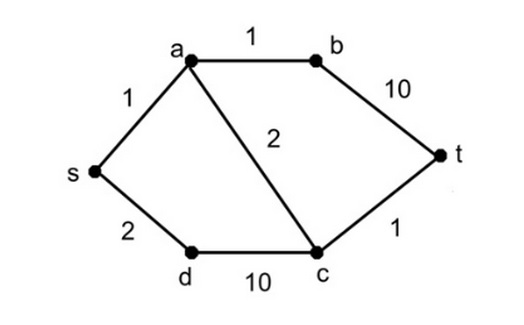

In onze eerste herhaling kijken we naar het dichtstbijzijnde knooppunt van s, wat op een afstand van 1 eenheid ligt. We noemen dit knooppunt a, en kijken naar de volgende aangrenzende knooppunten. b ligt op een afstand van 1 eenheid (2 vanaf het begin), c ligt op een afstand van 2 (3 vanaf het begin), en we hebben ook nog d, die ligt op 2 eenheden afstand vanaf het begin. Omdat we op zoek zijn naar de kortste afstand vanaf het begin worden we gedwongen om naar d te reizen vanaf s (2 eenheden), en daarom geven we d een waarde van 2. Bij de volgende herhaling van het algoritme, willen we van d naar c. Dat is op 10 eenheden afstand (en 12 vanaf het begin), maar we zien ook dat we vanaf plek a, naar c kunnen komen, in slechts 2 eenheden (3 vanaf het begin) en vanaf b in 1 eenheid (2 vanaf het begin). We zetten onze positie nu op b en wijzen een label van 2 toe (2 eenheden vanaf het begin).

Onze verkenner, gestationeerd op b, loopt nu tegen een teleurstelling aan. De enige manier om naar punt t te bewegen is op 10 eenheden afstand (en 12 vanaf het begin). Dat is meer dan de 2 eenheden vanaf punt a naar c (3 vanaf het begin) en hetzelfde geldt voor de afstand van s naar c via d, een mogelijkheid die we liever hebben (want we zijn bij c gearriveerd in maar 3 eenheiden en dat willen we liever dan 12 eenheden die het kost via d). We zijn nu bij c. Je zou denken dat het ingewikkeld is, maar dat is het echt niet. Het enige wat we doen is voorzichtige stappen maken van knooppunt naar knooppunt, terwijl we door het algoritme worden gedwongen altijd het kortste pad vanaf het begin te kiezen.

We kijken nog eens naar de weg tussen b en t: een afstand van 12 eenheden. Maar als je kijkt naar de afstand tussen c en t, zie je maar 1 eenheid. Dus als je vanaf punt s reist via c naar t, ben je in totaal maar 4 eenheden kwijt. Zo zie je dat een ongelooflijk explosief-complex-probleem, op simpele, elegante en zelfs intuïtieve wijze op papier wordt verklaard.

Meer voorbeelden:

Dijkstra zegt dat hij op dit idee kwam terwijl hij koffie zat te drinken op een terras. "Drie jaar daarna, in 1959 is het gepubliceerd," herinnert hij zich. "Die publicatie is nog steeds best aardig. Één van de redenen dat het zo'n fijne publicatie is, is dat het ontworpen is zonder pen en papier. Zonder pen en papier ben je bijna gedwongen om alle vermijdbare complicaties te vermijden. Uiteindelijk is dat algoritme, tot mijn verbazing, één van de mijlpalen voor mijn beroemdheid geweest."

Dit is hoe het systeem achter Google Maps werkt, of in ieder geval een variatie daarvan. Het is de manier hoe verschillende route-systemen überhaupt mogelijk gemaakt worden. Het vergt enkel de vaardigheid om door de ruis van mogelijkheden heen te kunnen kijken.